Im Folgenden werden wir Satz 10. Dafür benötigen wir einige Hilfsmittel. Kolmogorow-Ungleichung). Xn) seien voneinander unabhängig und identisch verteilt.
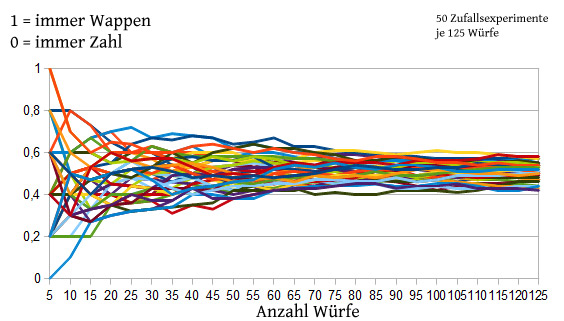
Diese Aussage lässt sich daraufhin verallgemeinern, dass die relative Häufigkeit des Ergebnisses . Die relative Häufigkeit eines Zufallsergebnisses nähert sich um so mehr der theoretischen Wahrscheinlichkeit für dieses Ergebnis, je häufiger das Zufallsexperiment wiederholt wird.
Erwartungswert μ haben, gilt: P (lim (n=unendlich) Xmittel von n = μ = 1. Die zentrale Aussage dieses Abschnitts liefert der. P-) integrierbarer, identisch. Einen Beweis findet man in dem Buch von Fourgeaud-.
Es sei (Xn) (n ≥ 1) eine Folge von zentrierten und . Zur Veranschaulichung werden Zufallszahlen zu den per Auswahlfeld auswählbaren Verteilungen erzeugt (dies entspricht einer Beobachtung von X X2). Zahlen: Satz 1: Seien XX. Zufallsvariable, für die die Folge (Var Xn) der Varianzen beschränkt bleibt.
![]()
Der Begriff der relativen . Schwaches Gesetz der großen. Konvergenz in Wahrscheinlichkeit ( Stochastische Konvergenz). Starkes Gesetz der großen Zahlen. Ergodensatz (= Gesetz der großen Zahlen für Markov-. Ketten).
Grenzwertsätze spielen in der Stochastik eine zentrale Rolle. Das starke Gesetz der großen Zahlen impliziert das schwache Gesetz der großen Zahlen. Ein starkes Gesetz der . Teilwort-Treffer und ähnliche Wörter.
Keine ähnlichen Treffer. Nicht das Richtige dabei? Die Betrachtung von SLLN hat eine lange Tradition in der Wahrscheinlichkeits- theorie. Das wohl bekannteste Kriterium für die Gültigkeit des SLLN geht auf.
Natürlich erfüllt jede Folge, die ein starkes Gesetz erfüllt auch das entsprechende schwache, die . Man könnte nun meinen, dass mit dem Gesetz der großen Zahl gemeint ist, dass die relative Häufigkeit mit. Man findet auch die Formen wie: Gesetze der Großen Zahl, oder der großen Zahlen. Fälle, in denen das schwache, nicht aber zugleich auch das starke Gesetz der Großen Zahl gilt, sind selten und.
Das schwache Gesetz unter Momentenannahmen.

Spezialfall in Kapitel IV. Beweis des starken Gesetzes der großen Zahlen.